My Research Ambition

I’m aiming to achieve the optimal trade-off between theory and learning.

Design algorithms that benefit both from rigorness of theory and flexibility of ML for different applications from combinatorial optimization to derivative pricing.

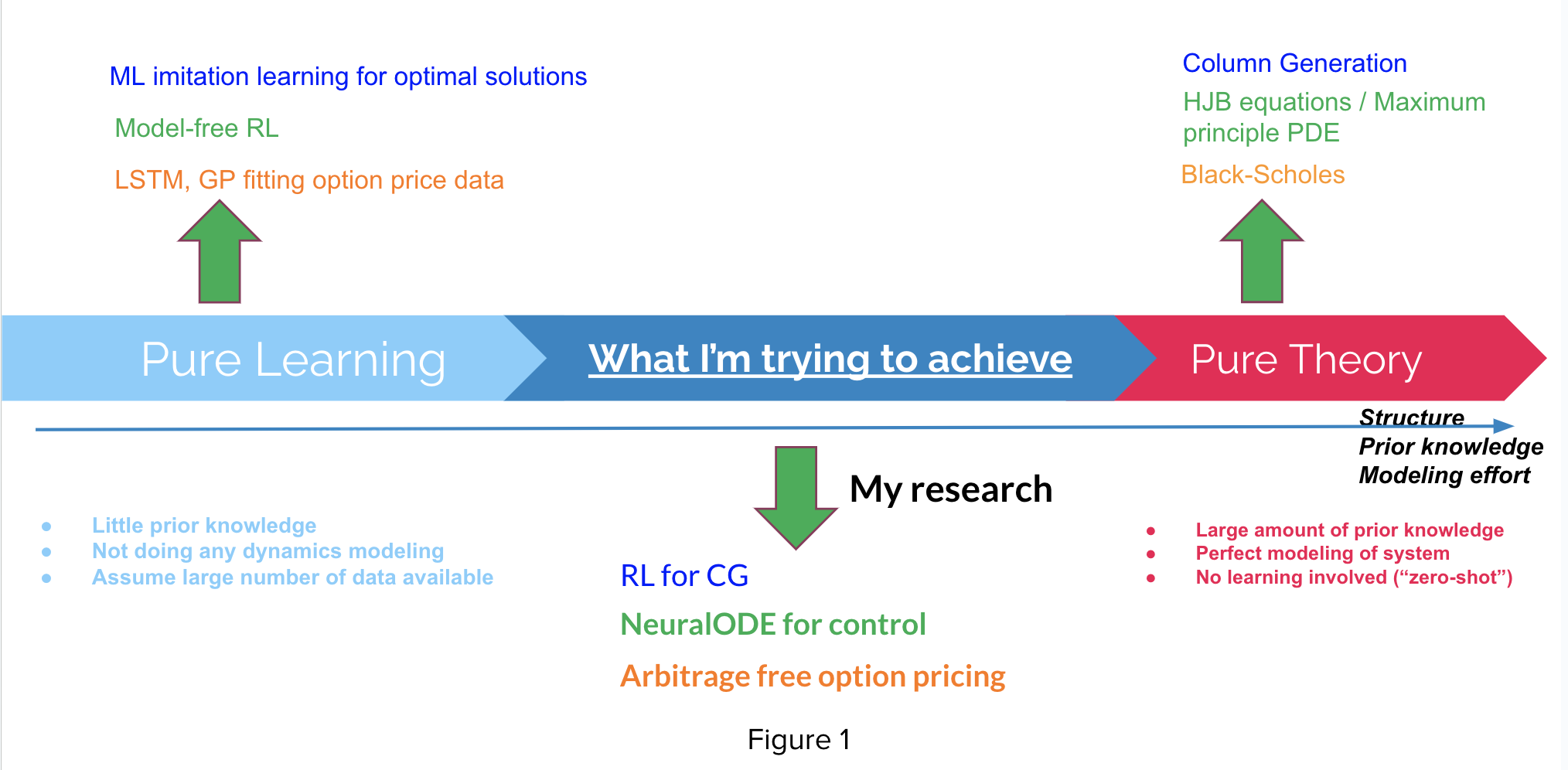
Example figure

This figure here shows my general research ambition. For any learning task, we can measure the amount of struture or prior knowledge we incorportate in the particular learning method we use, and we put an axis here. On the left-most of this axis, we have “pure learning” methods where we generally learn everything from scratch without any prior modeling about the system, and these methods are easy to set up but require a large amount of training. While on the right-most of this axis we have methods that are “pure theory”, where they generally require a huge effort in defining rigorous mathematical formulation of system dynamics, optimizations or optimality conditions, but once these things are set up, we could analytically solve for optimal solutions without any training.

I want to argue that all the methods on this axis is a particular method that WE CHOOSE to solve the problem (e.g. optimal control / optimization … ) at hand, and the optimal solution method in terms of prior modelling effort is unlikely to lie at the two end-point of this axis but somewhere in the middle for a variety of problems. If we can “theorize” “pure learning” methods or “learningrize” “pure theory” methods, we could potentially hit the optimal trade-off between rigorousness and flexibility, thus achieving optimal solutions or policies with relatively small amount of modelling effort as well as relatively small amount of training effort.

This is what I am trying to pursue in my master study and my research.

Below I will discuss my projects that are directly related to this topic.

ML (RL) for CG

For solving large scale optimization problem (color-coded by dark blue in figure above), “pure learning” method corresponds to train a large neural net directly to output optimal solution from solved optimizations, and a “pure theory” method correpsonds to traditional fixed-rule operational research algorithm column geneartion (CG). By trying to achieve an optimal trade-off between learning and theory, I embed a Reinfocement learning agent inside CG algorithm where agent learn to select varaible to enter the basis optimally, which led to my first project RLCG and my first publication in NeurIPS 2022. The sturcure / prior knowledge I use to achieve such trade-off is the fact that the solution process / optimal basis dynamics is given by CG algorithm rather than a pure generative process or an arbitrary mapping in “pure learning” methods.

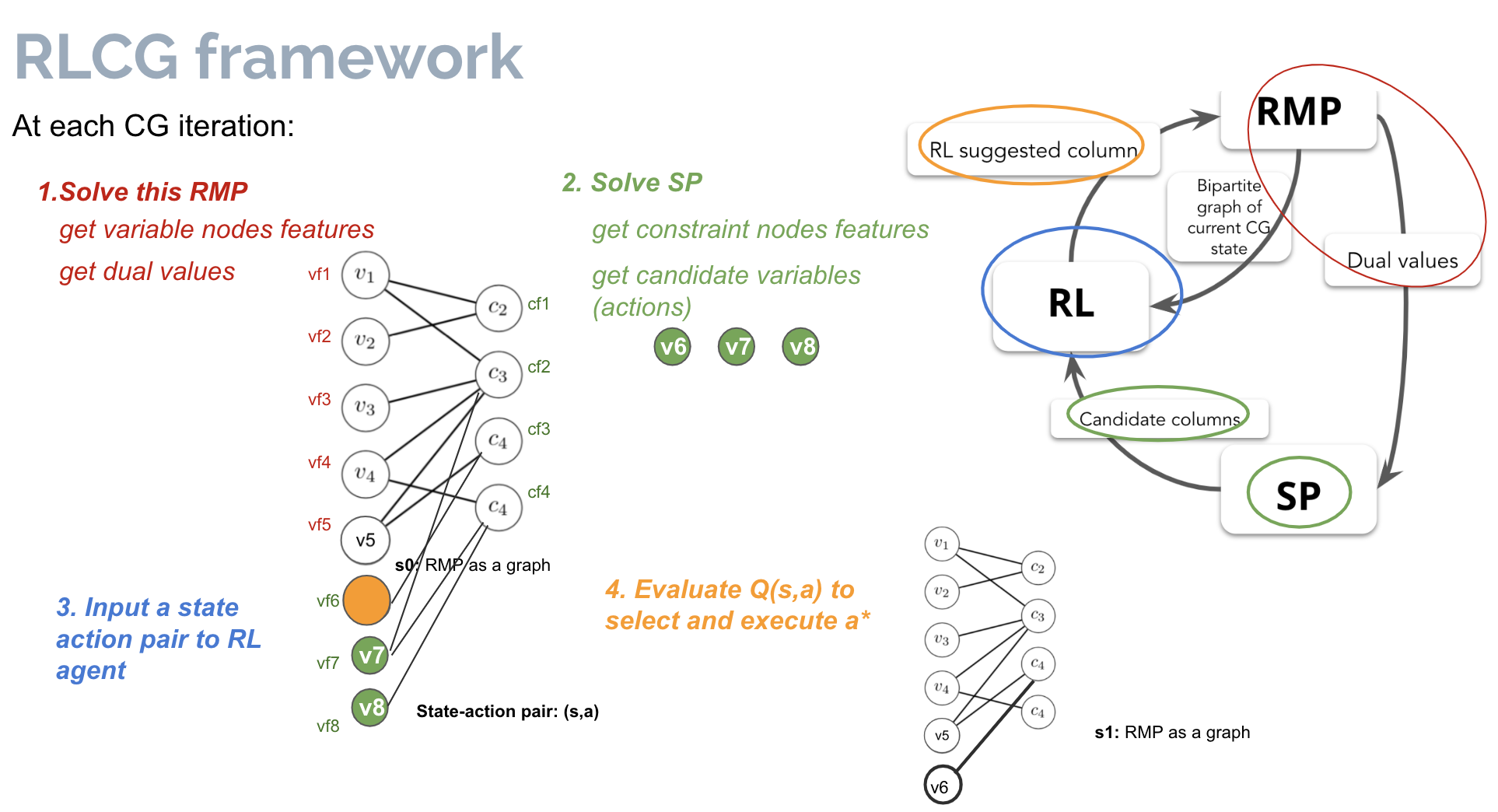
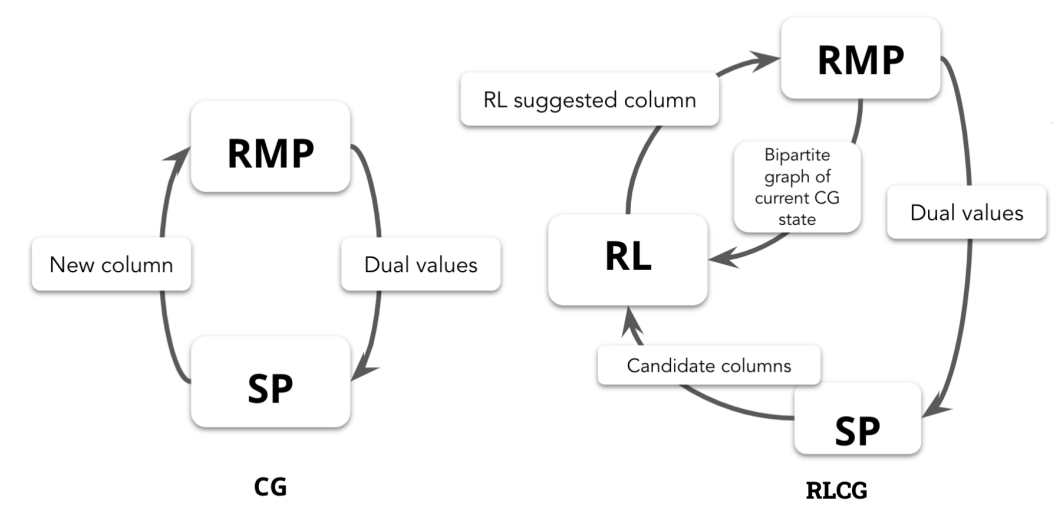
I embed a RL agent into column generation algorithm as follows: Example figure

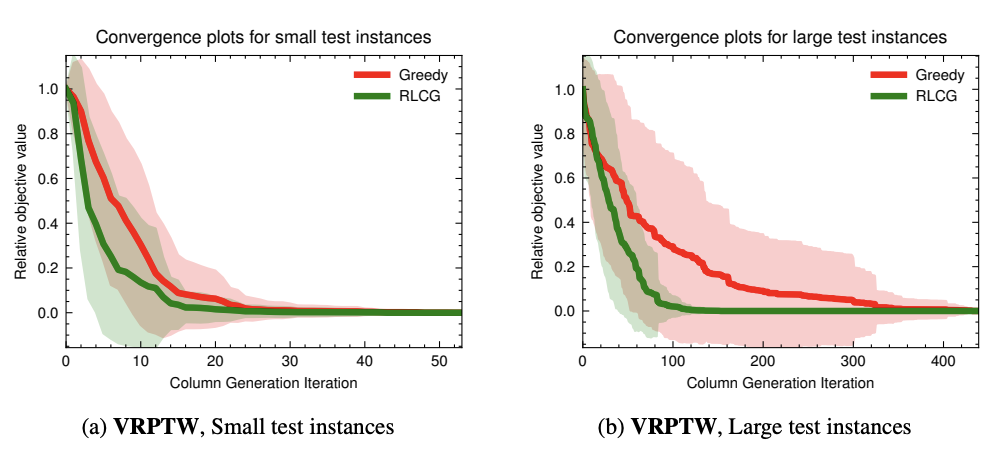
Thus the MDP components for RL are the following: Example figure

And I denote the above algorithms as RLCG, which is a method lies in the middle of the prior-modelling axis for solving large scale optimization problems. The results below are a direct comparison to the traditional operational research “pure theory” algorithm (denoted as greedy), which always select decision variables that have the most negetive reduced cost. RLCG beats the “pure theory” algorithm as it leads to faster convergence to optimal solutions for different optimization problems (only VRPTW shown here): Example figure

This work is published in NeurIPS 2022.

Machine learning for physical system control

For solving optimal control problem (color-coded by green in figure above), “pure learning” method corresponds to model-free RL where we use countless of interactions with the environment and reward signals to learn a value function or optimize a policy, and a “pure theory” method correpsonds to traditional optimal control method where we model system with controlled differential equations and then derive optimality condition using maximum principle or HJB which are in the form of PDEs, and solving those PDEs will generally lead to optimal controls / policy. By trying to achieve an optimal trade-off between learning and theory, I develop a neural ODE based learning algorithm that can learn the dynamics as well as optimal control at the same time from reletively small amount of interactions from the environment, which led to my thesis work (in preparation) and an application project of irrigation control. The sturcure / prior knowledge I use to achieve such trade-off is the fact that the systems I modelled here are continous in nature and the optimal control is conducted in a vector field.

The model that I use is a neural ODE model composed of both a dynamic learner (g) and a controller (h), and how we do a particular trajectory rollout or a prediction is the following: 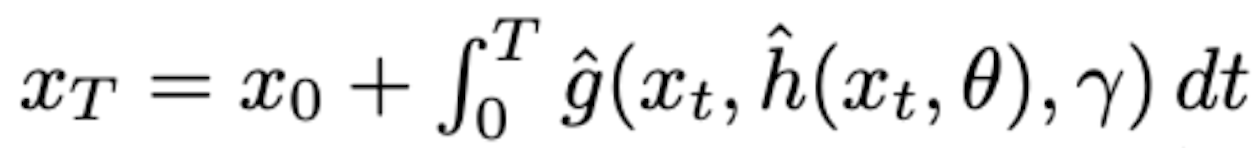Example figure The adjoint-method training of dynamic learner and controller is done alternatively so that in the end we are learning both the dynamics of the system as well as the optimal control in that dynamics for some objectives.

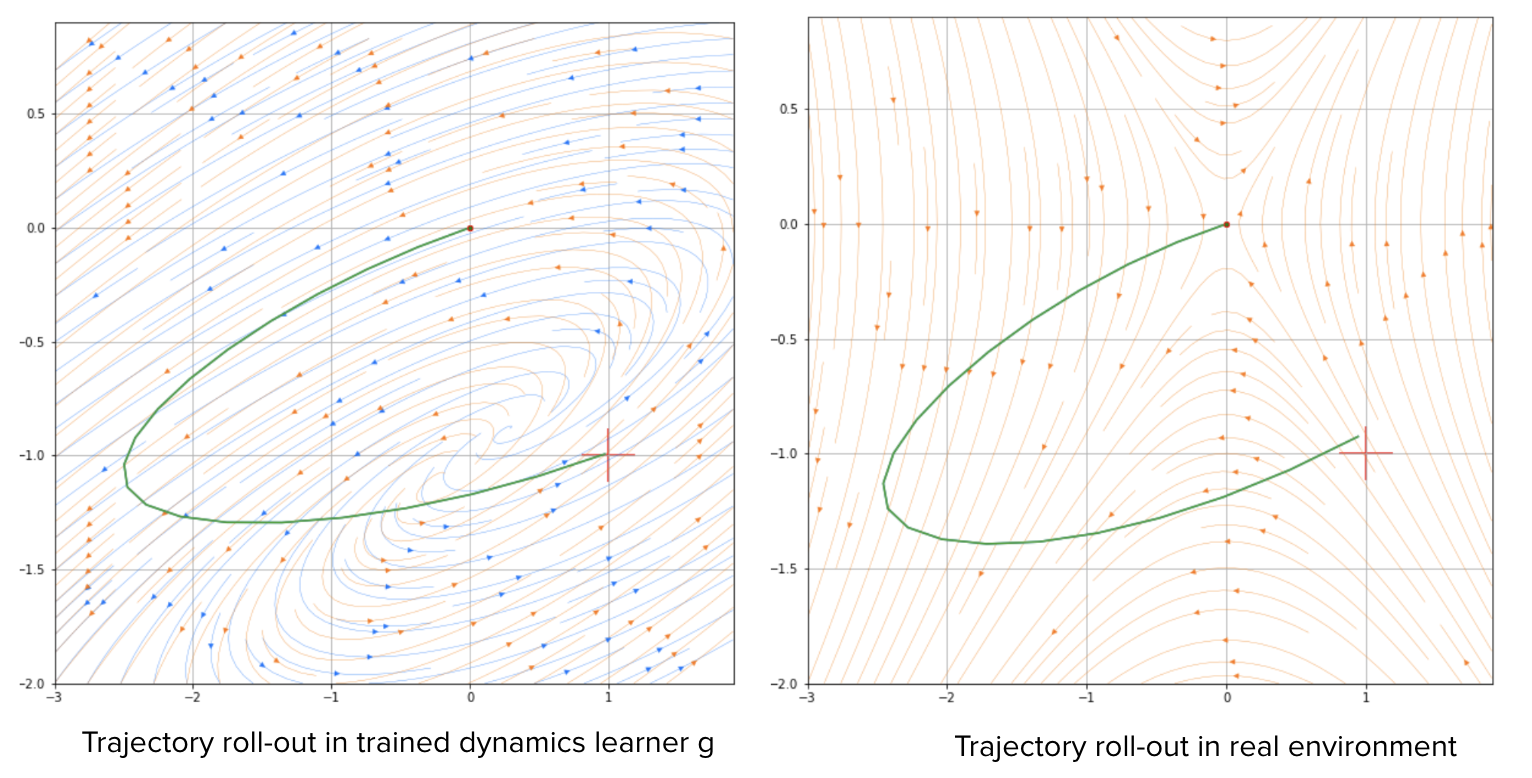
Here is an example of a simple control task in a 2-dim state (x) and 1-dim control (u) environment where the dynamics is given by dx/dt = f(x,u) = Ax + Bu, and we are trying to bring the system from state (0,0) to (1,-1) in shortest time: Example figure

We can see that we successfully bring state to (1,-1), and the vector field or the model we learned by h (shown in oranage arrows) is almost the same as the true dynamics or vector field (shown in blue). The learned controller h is almost the same as analytical optimal control from solving Maximum Principle, but we achieve this without having any knowledge of the true dynamics f(x,u).

By applying this new continous control method denote as NODEC to the irrigation control problem where dynamics of soil mositure level is given by a particular SDE, I was able to complete a project in India funded by IC-IMPARCS, where I could achieve similar soil moisture evolution and crop yield while saving more than 30% of total water usage compared to an optimization-based method (a “pure theory” method) and farmer’s original irrigations: 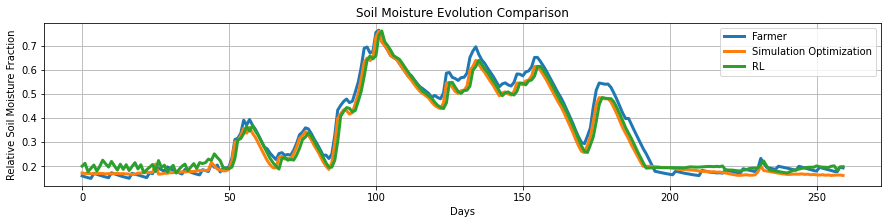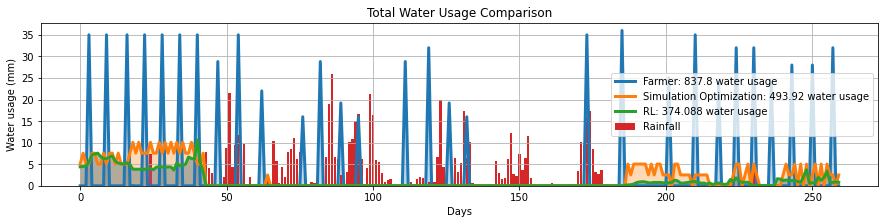Example figure Example figure

This method (NODEC) is a majority part of my master thesis and the application irrigation project report is in submission to Journal AGU: Advancing earth and space science.

Machine learning for no-arbitrage pricing

For modelling option price (color-coded by orange in figure above), “pure learning” method corresponds to fit a predictive model (either deterministic: LSTM or probabilistic: Gaussian process) using historical data, and a “pure theory” method corresponds to deriving no-arbitrage pricing following the dynamic-hedging arugments with an assumption of underlying asset price process model. By trying to achieve an optimal trade-off between learning and theory, I develop a ML pricing model that parameterize the arbitrage portfolio weights in some particular way so that the training leads to this model learning no-arbitrage prices even if the underlying asset price process is unknown, which led to my current collaboration with NYU Tandon department. The sturcure / prior knowledge I use to achieve such trade-off is the fact that the derivative prices generally, to a good approximation, respect no-arbitrage.

The pricing function learned by no-arbitrage ANN and the delta implied by the same function are the following: 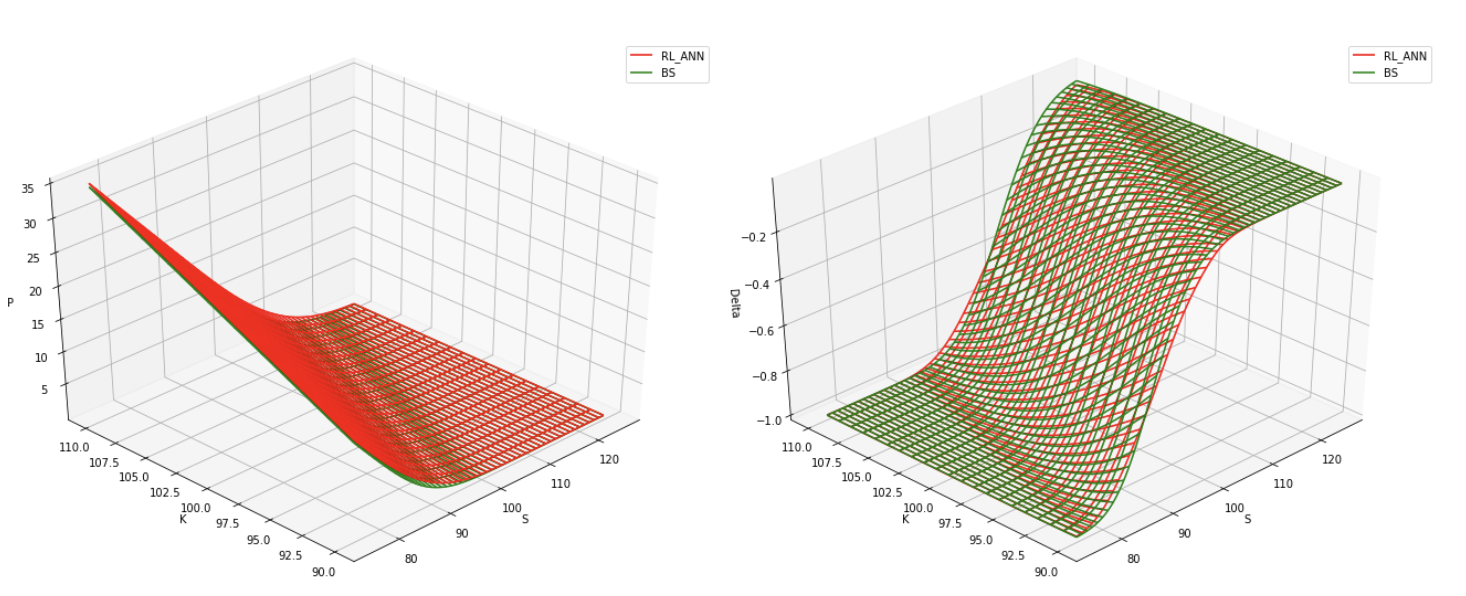Example figure where we recover the analytical no-arbitrage solution without having any knowledge about the true underlying asset process.

By combining this no-arbitrage training with a probabilistic predictive model, we are able to account for fluctuations away from no-arbitrage price in the real-world: Example figure where we assume that the real option prices distribution has no-arbitrage price mean and Gaussian distributed noise around that mean.

This work is a colloborative work with NYU Tandon department and it is in preparation for submission to Journal of Finance.

Recursive time series data augmentation

Time series with an unique history can be thought of as one realization of a generally unknown dynamical system. When we try to model such system or when we have some downstream tasks (e.g. time series forecast), what if we don’t have enough prior knowledge about the system to write down equation that governs dynamics of this system, and we also don’t have enough data (we just have one realization) to train a good ML model? How can we now find optimal trade-off between “pure theory”, which is completely unknown here, and “pure learning”, which is prone to overfit here due to lack of data?

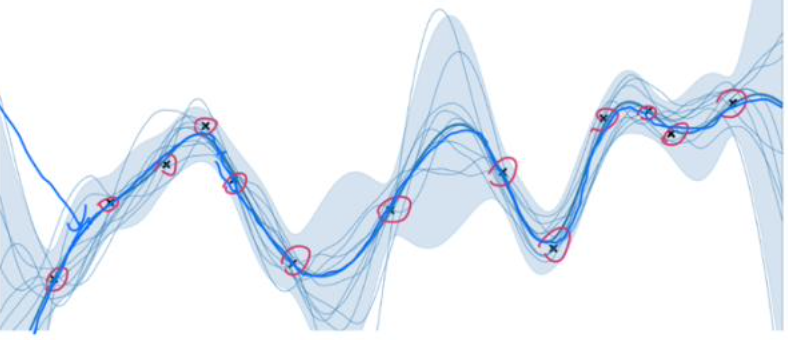
In this work, we assume dynamics can be represented by some unknown differential equations, which gives us linearity of the solution. That is, if we take one realization of such dynamics, and take another realization, then the linear combination of these two is again a valid solution or realization of the same dynamical system, and this property holds for all time intervals. We can get different realizations by controlling the weights of linear combination. These intuitions lead us to design a recursive interpolation based time series augmentation method that can augment extreme limited time serues dataset: 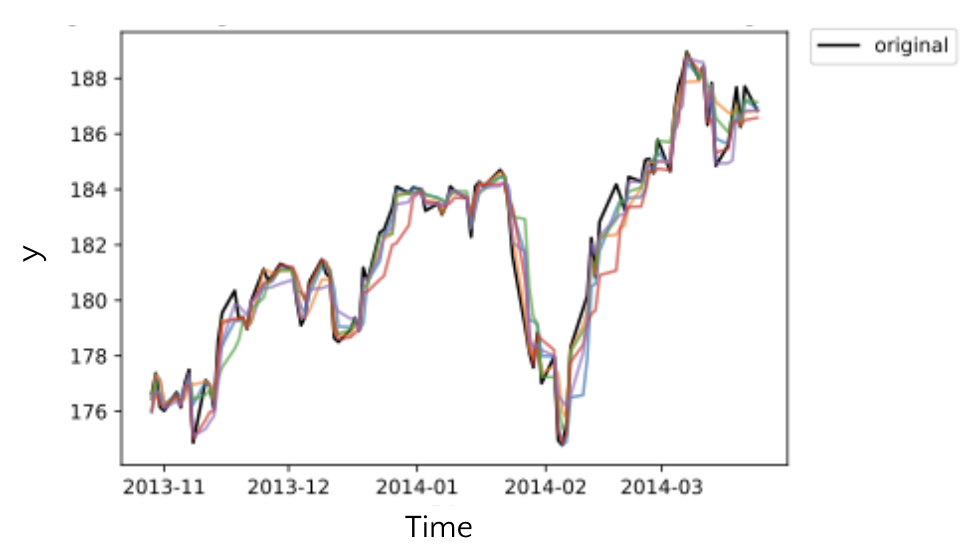Example figure We also prove that the augmented time series (the linear combinations) are bounded within some close distance to the original time series. However, for many cases, we would like to use the data augmentation to improve downstream learning tasks. For this, we also investigate the relation between learning performance, properties of the time series, and the neural network structure if we use our augmentation on the time series and use all these data to train this nerual network in downstream task.

The results of downstream task performance improvement is shown here: 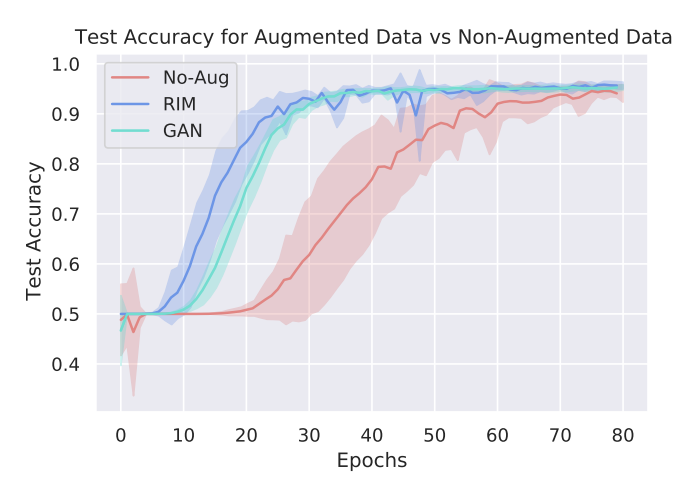Example figure where we show faster convergence and higher accuracy for downstream time series classification task, and we also study time series forecast and Reinforcement learning tasks in our work.

This work is published in ICLR 2023.

Other projects

I also work on other projects that are not a direct result of my goal from above, but still necessary tools for optimization and machine learning in general:

Quantum computing reducing systemic risk in financial networks

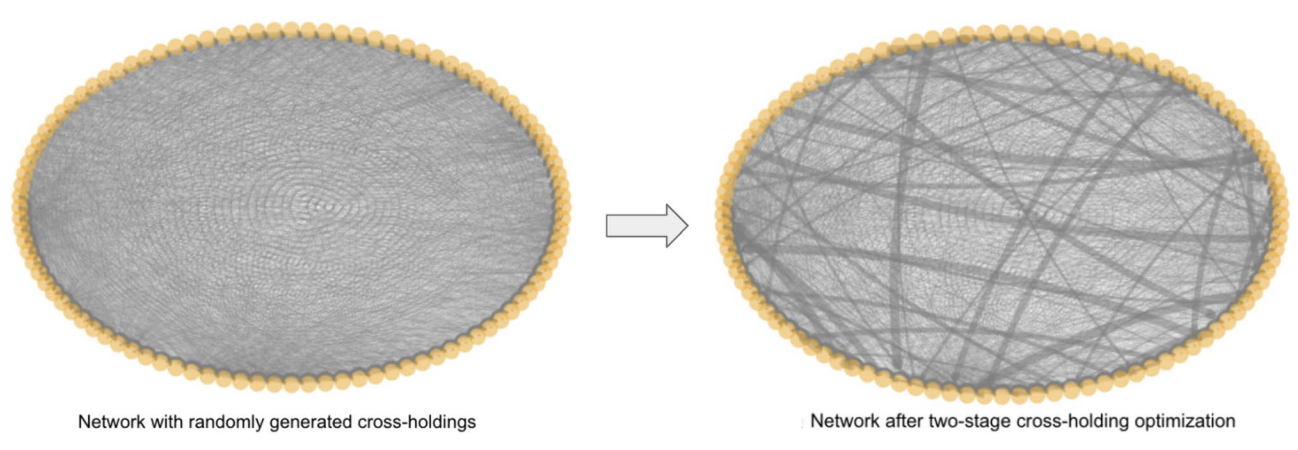In highly connected fnancial networks, the failure of a single or a few institution can cascade into additional bank failures: Example figure This systemic risk can be mitigated by adjusting the loans, holding shares, and other liabilities connecting institutions in a way that prevents cascading of failures. We are approaching the systemic risk problem by attempting to optimize the connections between the institutions with financially meaningful objective and constraints: Example figure We notice that the cascade failures first spread through highly connected groups (a module) and then spread between modules, as the connection between banks are the brigde that failure spreads. This intution leads us to the two-stage cascade prevention method, where we would first partition financial networks into modulues (community detection), and then optimize the module sub-network connections individually. In this way, we could
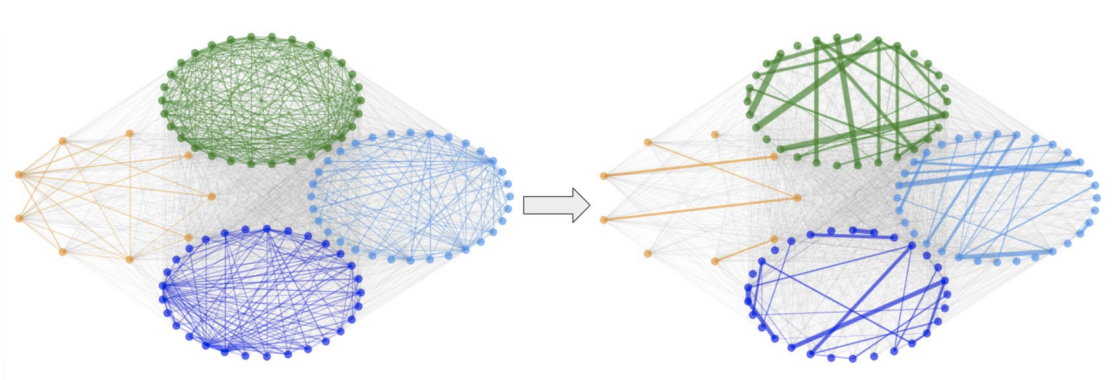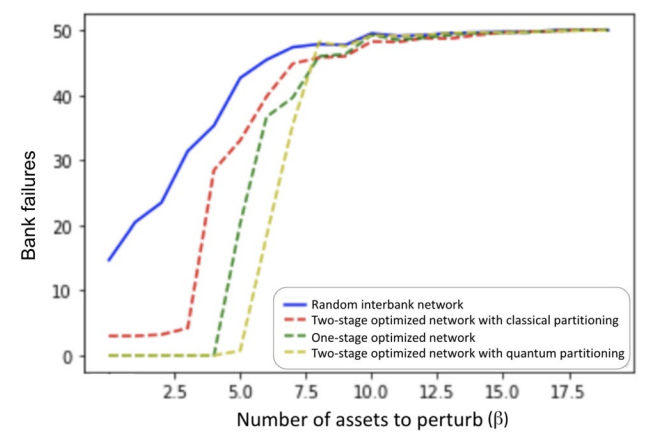
confine cascade failures from its source and keep the change of connections to a minimum. Example figure We apply quantum annealing as our heuristic for community detection where it can achieve more accurate partitioning with less time complexity. In particular, the modularity maximization is formullated as QUBO, mapped to Pegasus embedding and then solved in D-wave Advantage Quantum Annealer. 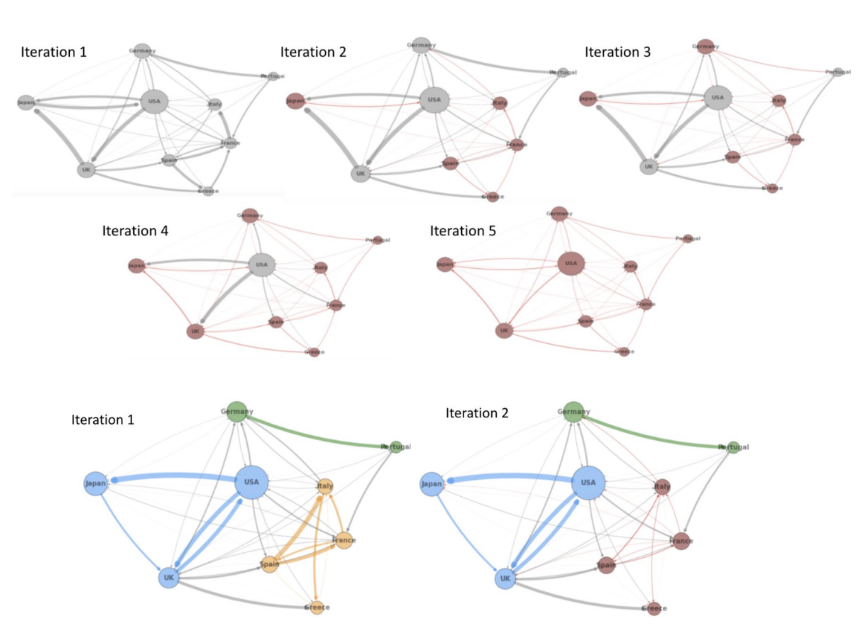The cascade simulation is mitigated as a result of our method, indicated by delayed phase transition in cascade failures where financial network can withstand higher perturbation without failure: Example figure We also demonstrate similar results using real-world data, where we perturb the original network and optimized network with the same level of perturbation, and compare the cascade results. We can see that all the institutions in the original network (top) fail as a result of the perturbation while in the optimized network (bottom) only few institutions fail. Example figure

This work is published in Nature Scientific Report on March, 2023.

Central bank cascade free control

This work is a direct extension from previous work on cascade failure mitigation. Instead of posing change in connectivities between institutions (banks in this case) as a hard constraints on banks, we respect the objective of banks which is maximizing their own profits. Therefore, central bank aims to give incentives or penalties as control signal to the system whose dynamics are given by the zero-sum games formulated as individual banks’ greedy optimizations.

We already studied some property of such dynamical system we are trying to control, where for some particular controls we have converged Nash Equalibrium of the low level optimizations (banks), while for some other controls we have osscilation of between equalibriums: Example figure We are now in the stage of learning an optimal control corresponds to cascade-free trajectory of this compicated dynamical system.